Variância
A variância é uma medida de dispersão que mostra o quão distante cada valor neste conjunto está do valor médio (média). Em outras palavras, é uma média dos quadrados das diferenças entre cada valor individual e a média do conjunto de dados. A fórmula para calcular a variância (para uma população) é:
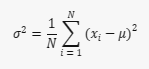
Onde:
- σ2 é a variância
- N é o número de observações
- xi é o valor da i-ésima observação
- μ é a média do conjunto de dados
Desvio Padrão
O desvio padrão é simplesmente a raiz quadrada da variância. Em termos de dispersão dos dados, o desvio padrão indica o quanto os dados estão espalhados em relação à média. A fórmula para calcular o desvio padrão (para uma população) é:

Onde:
- σ é o desvio padrão
- Os outros símbolos têm o mesmo significado que na fórmula da variância
Em resumo, a variância e o desvio padrão são medidas de dispersão que nos dão uma ideia de quão “espalhados” estão os dados em um conjunto. A variância é útil em várias análises estatísticas, e o desvio padrão é uma medida mais intuitiva por estar na mesma unidade que os dados.
Em outras palavras:
1. Definição:
Medidas de dispersão:
As medidas de dispersão fornecem informações sobre como os dados em um conjunto se distribuem em torno da média. Elas quantificam o quão dispersos os dados estão em relação ao valor central.
Variância:
A variância é a média dos quadrados das diferenças entre cada valor e a média do conjunto de dados. Ela indica o quão dispersos os dados estão em torno da média. Quanto maior a variância, maior a dispersão dos dados.
Desvio Padrão:
O desvio padrão é a raiz quadrada da variância. Ele representa a distância média entre os valores e a média, medida em unidades da mesma escala dos dados originais.
2. Cálculo:
Variância:
σ^2 = Σ[(x_i - μ)^2] / N
Onde:
- σ^2 é a variância
- Σ é o símbolo que significa “soma de”
- x_i é cada valor no conjunto de dados
- μ é a média do conjunto de dados
- N é o número de elementos no conjunto de dados
Desvio Padrão:
σ = √σ^2
Onde:
- σ é o desvio padrão
- σ^2 é a variância
3. Interpretação:
- Variância: A variância é expressa em unidades quadradas da variável original, o que dificulta a interpretação direta.
- Desvio Padrão: O desvio padrão é expressa nas mesmas unidades da variável original, facilitando a interpretação.
Regra de 68-95-99.7:
- Aproximadamente 68% dos dados estão dentro de 1 desvio padrão da média.
- 95% dos dados estão dentro de 2 desvios padrão da média.
- 99.7% dos dados estão dentro de 3 desvios padrão da média.
4. Aplicações:
- Comparar a dispersão de diferentes conjuntos de dados: Mesmo com médias semelhantes, conjuntos de dados podem ter diferentes dispersões.
- Avaliar a confiabilidade de intervalos de confiança: O desvio padrão é usado para calcular os intervalos de confiança, que indicam a probabilidade de a média real estar dentro de um determinado intervalo.
- Identificar outliers (valores atípicos): Valores que se distanciam significativamente da média (mais de 2 ou 3 desvios padrão) podem ser considerados outliers.
- Análise de risco em investimentos: O desvio padrão é utilizado para medir o risco de um investimento, ou seja, a volatilidade do seu retorno.
5. Considerações finais:
A variância e o desvio padrão são medidas estatísticas importantes para quantificar a dispersão dos dados em torno da média. A escolha da medida a ser utilizada dependerá dos objetivos da análise e do contexto dos dados.
Outras medidas de dispersão:
- Amplitude: Diferença entre o maior e o menor valor no conjunto de dados.
- Desvio médio absoluto: Média das distâncias absolutas entre cada valor e a média.
- Intervalo interquartil (IQR): Diferença entre o terceiro e o primeiro quartil.
Dicas:
- Utilize softwares estatísticos para facilitar o cálculo da variância e do desvio padrão.
- Considere o contexto dos dados ao interpretar a variância e o desvio padrão.
- Utilize outras medidas de dispersão em conjunto com a variância e o desvio padrão.
