Vamos entender o que é o coeficiente de correlação de Pearson e como calculá-lo.
Coeficiente de Correlação de Pearson
O coeficiente de correlação de Pearson é uma medida da força e direção da associação linear entre duas variáveis contínuas. O valor varia de -1 a 1, onde 1 significa uma correlação positiva perfeita, -1 uma correlação negativa perfeita, e 0 nenhuma correlação.
A fórmula para calcular o coeficiente de correlação de Pearson é:
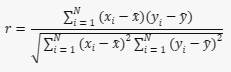
Onde:
- r é o coeficiente de correlação de Pearson
- N é o número de observações
- xi e yi são os valores das i-ésimas observações das variáveis x e y
- xˉ e yˉ são as médias de x e y
Interpretando o Coeficiente de Correlação de Pearson
A interpretação do coeficiente de correlação de Pearson depende do valor de r:
- Se r=1, há uma correlação positiva perfeita entre as duas variáveis. Isso significa que se uma variável aumenta, a outra também aumenta.
- Se r=−1, há uma correlação negativa perfeita entre as duas variáveis. Isso significa que se uma variável aumenta, a outra diminui.
- Se r=0, não há correlação entre as duas variáveis. Isso significa que as duas variáveis não se movem juntas.
Em outra palavras:
O coeficiente de correlação de Pearson (r) é uma medida estatística fundamental para quantificar a relação linear entre duas variáveis contínuas.
1. Cálculo do Coeficiente de Correlação de Pearson:
A fórmula para calcular o coeficiente de correlação de Pearson é a seguinte:
r = Σ[(x_i - μ_x)(y_i - μ_y)] / √[Σ(x_i - μ_x)^2 Σ(y_i - μ_y)^2]
Onde:
- r: Coeficiente de correlação de Pearson
- Σ: Símbolo que significa “soma de”
- x_i: Valor da variável X na i-ésima observação
- μ_x: Média da variável X
- y_i: Valor da variável Y na i-ésima observação
- μ_y: Média da variável Y
2. Interpretação do Coeficiente de Correlação de Pearson:
- Valor entre -1 e 1:
- r = 0: Ausência de correlação linear.
- r positivo: Correlação linear positiva (aumento em X acompanha aumento em Y).
- r negativo: Correlação linear negativa (aumento em X acompanha diminuição em Y).
- Força da relação:
- Valor absoluto de r (0 a 1) indica a força da relação linear.
- Quanto mais próximo de 1 (ou -1), mais forte a relação.
- Importante: Correlação não implica em causalidade.
3. Exemplo:
Considere os seguintes dados para as variáveis X (altura) e Y (peso) de 10 indivíduos:
| Indivíduo | X (altura) | Y (peso) |
|---|---|---|
| 1 | 1.70 | 70 |
| 2 | 1.80 | 80 |
| 3 | 1.90 | 90 |
| … | … | … |
Calculando o coeficiente de correlação de Pearson, obtemos r = 0.85.
Interpretação:
- Existe uma correlação linear positiva moderada entre altura e peso.
- Indivíduos mais altos tendem a ser mais pesados.
- Importante: Não podemos concluir que a altura causa o aumento do peso ou vice-versa.
4. Considerações Finais:
O coeficiente de correlação de Pearson é uma ferramenta valiosa para analisar a relação entre duas variáveis contínuas. No entanto, é importante lembrar que correlação não implica em causalidade.
Aplicações:
- Estatística: Testes de hipóteses, regressão linear, análise de variância.
- Economia: Análise de risco, previsão de mercado, modelagem de séries temporais.
- Ciências Sociais: Pesquisa de opinião, análise de comportamento, estudos de mercado.
Dicas:
- Utilize softwares estatísticos para calcular o coeficiente de correlação de Pearson.
- Considere o contexto dos dados ao interpretar o coeficiente de correlação.
- Utilize outras medidas estatísticas para complementar a análise.
