Se você multiplicar todos os dados em um conjunto por uma constante, a variância desse conjunto de dados será multiplicada pelo quadrado dessa constante.
Vamos considerar um conjunto de dados X com n elementos x1,x2,…,xn e uma constante c. Se multiplicarmos cada elemento de X por c, obteremos um novo conjunto de dados Y com elementos y1,y2,…,yn onde yi=c⋅xi para todo i.
A variância de X é dada por:
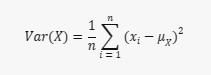
onde μX é a média de X.
A variância de Y é:
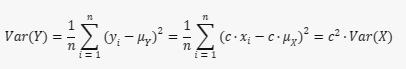
Portanto, a variância do conjunto de dados será multiplicada pelo quadrado da constante. Isso ocorre porque a variância mede a dispersão dos dados, e quando você multiplica os dados por uma constante, você está “esticando” ou “comprimindo” os dados, o que afeta sua dispersão.
Em outras palavras:
Se multiplicarmos todos os dados de um conjunto por uma constante k, a variância do conjunto também será multiplicada por k^2.
Explicação:
A variância é a média dos quadrados das diferenças entre cada valor e a média. Ao multiplicarmos todos os valores por k, as diferenças entre os valores e a média também serão multiplicadas por k. No entanto, ao calcularmos o quadrado dessas diferenças, o efeito de k será amplificado, resultando em um aumento da variância por k^2.
Exemplo:
Considere um conjunto de dados com os valores {1, 2, 3} e variância de 2.
- Média: (1 + 2 + 3) / 3 = 2
- Variância: [(1-2)^2 + (2-2)^2 + (3-2)^2] / 3 = 2
Se multiplicarmos todos os valores por 2, obtemos o novo conjunto {2, 4, 6}.
- Nova média: (2 + 4 + 6) / 3 = 4
- Nova variância: [(2-4)^2 + (4-4)^2 + (6-4)^2] / 3 = 8
Observe que a nova variância é 4 vezes maior que a variância original. Isso confirma que a variância é multiplicada por k^2 quando todos os dados são multiplicados por k.
Aplicações:
- Análise de risco em investimentos: Se o retorno de um investimento for multiplicado por uma constante (por exemplo, ao investir em ações de uma empresa que se funde com outra), a variância do retorno também será multiplicada por k^2. Isso significa que o risco do investimento também aumenta.
- Escalamento de dados: Ao transformar dados em diferentes unidades, a variância também pode ser escalada. É importante considerar esse efeito ao interpretar a variância de dados transformados.
Considerações finais:
Compreender o efeito da multiplicação dos dados por uma constante na variância é essencial para interpretar corretamente medidas estatísticas e tomar decisões informadas em diferentes contextos.
Dicas:
- Utilize softwares estatísticos para facilitar o cálculo da variância.
- Considere o contexto dos dados ao interpretar a variância.
- Utilize outras medidas de dispersão em conjunto com a variância, como o desvio padrão e o IQR.
