Vamos entender o que são assimetria e curtose.
Assimetria
A assimetria é uma medida que descreve a falta de simetria em uma distribuição de dados. Uma distribuição é simétrica se, quando você a dobra ao meio, as duas metades se alinham perfeitamente. Se elas não se alinham, a distribuição é assimétrica.
A assimetria pode ser positiva ou negativa, dependendo de qual lado da distribuição tem a cauda mais longa. Uma assimetria positiva significa que a cauda à direita da média é mais longa, indicando que há mais valores acima da média. Uma assimetria negativa significa que a cauda à esquerda da média é mais longa, indicando que há mais valores abaixo da média.
A fórmula para calcular a assimetria é:
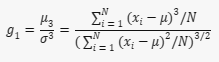
Onde:
- g1 é a assimetria
- μ3 é o terceiro momento central (a média dos cubos das diferenças entre cada valor e a média)
- σ é o desvio padrão
- N é o número de observações
- xi é o valor da i-ésima observação
- μ é a média do conjunto de dados
Curtose
A curtose é uma medida que descreve o “achatamento” ou “pico” de uma distribuição de dados. Uma distribuição com curtose alta tem um pico mais agudo e caudas mais pesadas, enquanto uma distribuição com curtose baixa é mais achatada.
A fórmula para calcular a curtose é:
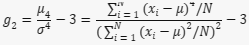
Onde:
- g2 é a curtose
- μ4 é o quarto momento central (a média das quartas potências das diferenças entre cada valor e a média)
- Os outros símbolos têm o mesmo significado que na fórmula da assimetria
1. Assimetria: Medindo o Desequilíbrio da Distribuição
A assimetria quantifica o desequilíbrio da distribuição dos dados em relação à sua média.
- Simétrica: Distribuição uniforme em ambos os lados da média.
- Assimétrica à direita (positiva): Maior concentração de dados à esquerda da média.
- Assimétrica à esquerda (negativa): Maior concentração de dados à direita da média.
Coeficiente de Assimetria:
- Medida quantitativa da assimetria.
- Valor zero indica simetria.
- Valores positivos indicam assimetria à direita.
- Valores negativos indicam assimetria à esquerda.
Interpretação da Assimetria:
- Útil para identificar outliers e compreender a forma da distribuição dos dados.
- Em pesquisas científicas, a assimetria pode indicar a presença de vieses ou fatores que afetam a distribuição dos dados.
2. Curtose: Avaliando a “Altura” da Distribuição
A curtose informa o quão “achatada” ou “pontiaguda” é a distribuição dos dados em comparação com uma distribuição normal.
- Curtose normal (mesocúrtica): Distribuição similar à normal.
- Curtose baixa (platicúrtica): Distribuição mais achatada que a normal.
- Curtose alta (leptocúrtica): Distribuição mais pontiaguda que a normal.
Coeficiente de Curtose:
- Medida quantitativa da curtose.
- Valor zero indica curtose normal.
- Valores negativos indicam curtose baixa.
- Valores positivos indicam curtose alta.
Interpretação da Curtose:
- Útil para identificar outliers e compreender a forma da distribuição dos dados.
- Em análises financeiras, a curtose pode ser utilizada para avaliar o risco de um investimento.
3. Correlação: Desvendando a Relação entre Variáveis
A correlação quantifica a relação linear entre duas variáveis.
- Coeficiente de correlação (r): Valor entre -1 e 1.
- r = 0: Ausência de correlação linear.
- r positivo: Correlação positiva (aumento em uma variável acompanha o aumento na outra).
- r negativo: Correlação negativa (aumento em uma variável acompanha a diminuição na outra).
Interpretação da Correlação:
- Força da relação: Valor absoluto de r (0 a 1).
- Direção da relação: Sinal de r (positivo ou negativo).
- Importante: Correlação não implica em causalidade.
4. Considerações Finais:
Assimetria, curtose e correlação são medidas importantes para descrever e compreender a forma e a relação entre distribuições de dados.
Aplicações:
- Estatística: Testes de hipóteses, regressão linear, análise de variância.
- Economia: Análise de risco, previsão de mercado, modelagem de séries temporais.
- Ciências Sociais: Pesquisa de opinião, análise de comportamento, estudos de mercado.
Dicas:
- Utilize softwares estatísticos para calcular os coeficientes de assimetria, curtose e correlação.
- Considere o contexto dos dados ao interpretar as medidas.
- Utilize outras medidas estatísticas para complementar a análise.
