Vamos explorar o conceito de probabilidade condicional e independência.
Entendendo Facilmente
Vamos começar com um exemplo simples. Imagine que você tem uma caixa de frutas com 3 maçãs e 2 laranjas. Se você pegar uma fruta sem olhar, a probabilidade de pegar uma maçã é de 3/5. Agora, suponha que alguém olhou na caixa e te disse que você não pegou uma laranja. Isso muda a probabilidade de você ter pegado uma maçã? Sim! Agora a probabilidade é de 1, porque só restam maçãs. Isso é probabilidade condicional.
Agora, imagine que você tem duas caixas. Uma tem 3 maçãs e 2 laranjas, e a outra tem 4 bananas e 1 abacaxi. Se você escolher uma caixa aleatoriamente e pegar uma fruta, a probabilidade de pegar uma maçã da primeira caixa não afeta a probabilidade de pegar uma banana da segunda caixa. Isso é independência.
Explicação
A probabilidade condicional de um evento B é a probabilidade de que o evento ocorra dado o conhecimento de que um evento A já ocorreu. Isso é expresso matematicamente como P(B|A), que lê-se “probabilidade de B dado A”.
A independência de dois eventos A e B é uma situação especial de probabilidade condicional. Nesse caso, o evento A ocorrer (ou não ocorrer) não tem efeito sobre a probabilidade de B ocorrer, e vice-versa. Isso é expresso matematicamente como P(A ∩ B) = P(A)P(B).
Probabilidade Condicional: A Influência Entre Eventos
A probabilidade condicional quantifica a chance de um segundo evento (B) acontecer depois que um primeiro evento (A) já ocorreu. Ela leva em consideração a influência que o primeiro evento exerce sobre a probabilidade do segundo.
Formalmente:
Probabilidade condicional de B dado A = Probabilidade de A e B / Probabilidade de A
Interpretação:
- Valores entre 0 e 1:
- 0: A ocorrência de A não influencia a probabilidade de B.
- 1: A ocorrência de A torna B certo.
- Valores entre 0 e 1: A ocorrência de A aumenta ou diminui a probabilidade de B.
- Exemplo: Retirada de bolas de uma urna.
- Urna com 3 bolas vermelhas e 2 bolas azuis.
- Probabilidade de retirar uma bola vermelha = 3/5.
- Probabilidade de retirar uma segunda bola vermelha depois de retirar uma bola vermelha (sem repor a bola) = 2/4 = 1/2.
Cálculo:
- Regra da multiplicação:
Probabilidade de A e B = Probabilidade de A * Probabilidade condicional de B dado A
- Regra da divisão:
Probabilidade condicional de B dado A = Probabilidade de A e B / Probabilidade de A
Independência: A Autonomia dos Eventos
Dois eventos são considerados independentes se a ocorrência de um não interfere na probabilidade do outro. Ou seja, a chance de um evento acontecer não é alterada pelo fato de o outro evento ter acontecido ou não.
Formalmente:
Dois eventos A e B são independentes se:
Probabilidade condicional de B dado A = Probabilidade de B
Interpretação:
- Eventos independentes: A ocorrência de um não fornece informação sobre a probabilidade do outro.
- Eventos dependentes: A ocorrência de um fornece informação sobre a probabilidade do outro.
Exemplos:
- Lançamento de duas moedas:
- Probabilidade de obter cara na primeira moeda = 1/2.
- Probabilidade de obter cara na segunda moeda = 1/2.
- Os eventos são independentes: a probabilidade de obter cara na segunda moeda não é afetada pelo resultado da primeira moeda.
- Sorteio de duas cartas de um baralho:
- Probabilidade de retirar um ás na primeira carta = 4/52 = 1/13.
- Probabilidade de retirar um rei na segunda carta depois de retirar um ás (sem repor a carta) = 3/51.
- Os eventos são dependentes: a probabilidade de retirar um rei na segunda carta é menor porque o ás não foi reposto.
Relação Entre Probabilidade Condicional e Independência
- Eventos independentes:
- Probabilidade condicional de B dado A = Probabilidade de B.
- A ocorrência de A não fornece informação sobre a probabilidade de B.
- Eventos dependentes:
- Probabilidade condicional de B dado A ≠ Probabilidade de B.
- A ocorrência de A fornece informação sobre a probabilidade de B.
Aplicações
- Medicina: Diagnosticar doenças com base em sintomas e resultados de testes.
- Finanças: Avaliar o risco de investimentos.
- Engenharia: Calcular a confiabilidade de sistemas.
- Ciência da Computação: Desenvolver sistemas de inteligência artificial.
Considerações Finais
Compreender a probabilidade condicional e a independência de eventos é fundamental para diversos campos do conhecimento. Ao dominar esses conceitos, você estará apto a analisar situações complexas e tomar decisões mais informadas.
Dúvidas?
Sinta-se à vontade para perguntar sobre qualquer aspecto relacionado à probabilidade condicional e independência, como cálculo em diferentes situações, exemplos práticos, interpretações e aplicações em diferentes áreas do conhecimento.
Definição e Cálculo da Probabilidade Condicional: Uma Jornada Detalhada
1. Definição Essencial:
A probabilidade condicional quantifica a chance de um evento B acontecer depois que outro evento A já ocorreu. Ela considera a influência que a ocorrência de A exerce sobre a probabilidade de B.
Formalmente:
- Probabilidade condicional de B dado A: P(B|A)
- Cálculo:
P(B|A) = P(A ∩ B) / P(A)
2. Interpretação da Probabilidade Condicional:
- Valores entre 0 e 1:
- 0: A ocorrência de A não influencia a probabilidade de B.
- 1: A ocorrência de A torna B certo.
- Valores entre 0 e 1: A ocorrência de A aumenta ou diminui a probabilidade de B.
3. Exemplos Práticos:
- Lançamento de duas moedas:
- Probabilidade de obter cara na primeira moeda = 1/2.
- Probabilidade de obter cara na segunda moeda depois de obter cara na primeira moeda = 1/2.
- A ocorrência de cara na primeira moeda não influencia a probabilidade de cara na segunda moeda (eventos independentes).
- Retirada de bolas de uma urna:
- Urna com 3 bolas vermelhas e 2 bolas azuis.
- Probabilidade de retirar uma bola vermelha = 3/5.
- Probabilidade de retirar uma segunda bola vermelha depois de retirar uma bola vermelha (sem repor a bola) = 2/4 = 1/2.
- A ocorrência de retirar uma bola vermelha aumenta a probabilidade de retirar uma segunda bola vermelha (eventos dependentes).
4. Cálculo da Probabilidade Condicional:
- Regra da Multiplicação:
P(A ∩ B) = P(A) * P(B|A)
- Regra da Divisão:
P(B|A) = P(A ∩ B) / P(A)
5. Aplicações da Probabilidade Condicional:
- Medicina: Diagnosticar doenças com base em sintomas e resultados de testes.
- Finanças: Avaliar o risco de investimentos.
- Engenharia: Calcular a confiabilidade de sistemas.
- Ciência da Computação: Desenvolver sistemas de inteligência artificial.
6. Considerações Finais:
A probabilidade condicional é uma ferramenta poderosa para analisar a influência de eventos entre si. Ao dominar esse conceito, você estará apto a tomar decisões mais precisas em diversas áreas do conhecimento.
Definição Essencial de Eventos Independentes
Eventos independentes são aqueles em que a ocorrência de um não interfere na probabilidade do outro. Ou seja, a chance de um evento acontecer não é alterada pelo fato de o outro evento ter acontecido ou não.
Formalmente:
Dois eventos A e B são considerados independentes se:
- Probabilidade condicional de B dado A = Probabilidade de B:
P(B|A) = P(B)
- Equivalentemente:
P(A ∩ B) = P(A) * P(B)
Interpretação:
- Eventos independentes: A ocorrência de um não fornece informação sobre a probabilidade do outro.
- Eventos dependentes: A ocorrência de um fornece informação sobre a probabilidade do outro.
Exemplos Práticos:
- Lançamento de duas moedas:
- Probabilidade de obter cara na primeira moeda = 1/2.
- Probabilidade de obter cara na segunda moeda = 1/2.
- Os eventos são independentes: a probabilidade de obter cara na segunda moeda não é afetada pelo resultado da primeira moeda.
- Sorteio de duas cartas de um baralho:
- Probabilidade de retirar um ás na primeira carta = 4/52 = 1/13.
- Probabilidade de retirar um rei na segunda carta depois de retirar um ás (sem repor a carta) = 3/51.
- Os eventos são dependentes: a probabilidade de retirar um rei na segunda carta é menor porque o ás não foi reposto.
Aplicações:
- Cálculo de probabilidades: Simplificar o cálculo de probabilidades de eventos compostos.
- Modelagem: Modelar situações reais usando a teoria da probabilidade.
- Simulação: Simular eventos aleatórios em computadores.
Considerações Finais:
Compreender a independência de eventos é fundamental para diversos campos do conhecimento. Ao dominar esse conceito, você estará apto a analisar situações complexas e tomar decisões mais informadas.
Cálculo da Probabilidade de Eventos Independentes: Uma Jornada Simplificada
Ao lidar com eventos independentes, o cálculo da probabilidade se torna mais simples, pois a ocorrência de um evento não interfere na probabilidade do outro.
1. Regra Fundamental:
A probabilidade de dois eventos independentes A e B ocorrerem juntos é o produto das probabilidades individuais de cada evento:
P(A ∩ B) = P(A) * P(B)
2. Interpretação Essencial:
- P(A ∩ B): Probabilidade de A e B acontecerem juntos.
- P(A): Probabilidade de A acontecer.
- P(B): Probabilidade de B acontecer.
3. Exemplos Práticos:
- Lançamento de duas moedas:
- Probabilidade de cara na primeira moeda = 1/2.
- Probabilidade de cara na segunda moeda = 1/2.
- Probabilidade de obter cara nas duas moedas = (1/2) * (1/2) = 1/4.
- Sorteio de duas cartas de um baralho (com reposição):
- Probabilidade de retirar um ás na primeira carta = 4/52 = 1/13.
- Probabilidade de retirar um rei na segunda carta = 4/52 = 1/13.
- Probabilidade de retirar um ás e depois um rei = (1/13) * (1/13) = 1/169.
4. Considerações Finais:
Ao utilizar a regra fundamental para eventos independentes, você pode calcular de maneira rápida e eficiente a probabilidade de eventos compostos. Essa ferramenta é essencial em diversas áreas do conhecimento, como matemática, estatística, probabilidade e finanças.
Desvendando o Teorema de Bayes: Atualizando a Probabilidade à Luz de Novas Evidências
O Teorema de Bayes é uma poderosa ferramenta da teoria da probabilidade que permite atualizar a probabilidade de um evento (hipótese) considerando informações adicionais (evidências).
1. Formalização:
O teorema de Bayes relaciona a probabilidade condicional posterior P(B|A), a probabilidade condicional anterior P(A|B), a probabilidade marginal de A (P(A)) e a probabilidade marginal de B (P(B)):
P(B|A) = [ P(A|B) * P(B) ] / P(A)
- P(B|A): Probabilidade condicional posterior – probabilidade de B ocorrer dado que A já ocorreu (atualizada com a evidência A).
- P(A|B): Probabilidade condicional anterior – probabilidade de A ocorrer dado que B já ocorreu (informação inicial sobre a relação entre A e B).
- P(B): Probabilidade marginal de B – probabilidade de B ocorrer sem considerar A.
- P(A): Probabilidade marginal de A – probabilidade de A ocorrer sem considerar B.
2. Interpretação:
Imagine que você tem uma hipótese (A) e novas evidências (B) chegam. O teorema de Bayes permite recalcular a probabilidade da hipótese (A) considerando essas evidências.
3. Exemplos Práticos:
- Diagnóstico médico:
- Doença (A)
- Sintoma (B)
- Classificação de spam em e-mail:
- Spam (A)
- Palavra-chave no e-mail (B)
4. Importância:
O Teorema de Bayes permite uma abordagem mais dinâmica da probabilidade, atualizando as crenças iniciais à luz de novas informações.
5. Considerações Finais:
O Teorema de Bayes tem amplas aplicações em diversos campos, como:
- Medicina
- Finanças
- Inteligência artificial
- Ciência da computação
Como a probabilidade condicional se relaciona com o Teorema de Bayes?
O Teorema de Bayes é uma fórmula que descreve como atualizar as probabilidades de hipóteses quando são obtidas evidências. Ele é fundamental para a compreensão da inferência estatística e é baseado no conceito de probabilidade condicional.
Aqui está a fórmula do Teorema de Bayes:
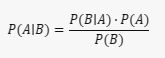
Onde:
- P(A∣B) é a probabilidade condicional de A dado B. É chamada de probabilidade a posteriori.
- P(B∣A) é a probabilidade condicional de B dado A. É chamada de verossimilhança.
- P(A) e P(B) são as probabilidades de A e B independentemente de cada um. P(A) é chamada de probabilidade a priori.
Então, a probabilidade condicional é usada para calcular a probabilidade a posteriori, que é a probabilidade de uma hipótese A dado que a evidência B é verdadeira. Isso é feito usando a probabilidade a priori e a verossimilhança.
O que acontece se os eventos A e B são mutuamente exclusivos? Eles podem ser independentes?
Imagine que você tem uma moeda e um dado. O evento A é “a moeda cai em cara” e o evento B é “o dado mostra 6”. Esses eventos são independentes porque o resultado da moeda não afeta o resultado do dado.
Agora, vamos considerar dois eventos mutuamente exclusivos. O evento A é “a moeda cai em cara” e o evento B é “a moeda cai em coroa”. Esses eventos são mutuamente exclusivos porque ambos não podem acontecer ao mesmo tempo. Se a moeda cai em cara, ela não pode cair em coroa, e vice-versa.
Eventos mutuamente exclusivos não podem ser independentes. Aqui está o porquê:
Eventos A e B são mutuamente exclusivos se eles não podem ocorrer ao mesmo tempo. Isso é, se A ocorre, então B não pode ocorrer, e vice-versa. Matematicamente, isso é expresso como P(A∩B)=0.
Eventos A e B são independentes se a ocorrência de A não afeta a probabilidade de B, e vice-versa. Matematicamente, isso é expresso como P(A∩B)=P(A)P(B).
Se A e B são mutuamente exclusivos, então P(A∩B)=0. Mas se A e B são independentes, então P(A∩B)=P(A)P(B), que não é igual a zero (a menos que P(A) ou P(B) seja zero). Portanto, se A e B são mutuamente exclusivos, eles não podem ser independentes, a menos que a probabilidade de um deles seja zero.
Como você pode testar a independência de dois eventos?
Para testar a independência de dois eventos, você pode usar a definição matemática de eventos independentes. Dois eventos A e B são independentes se a ocorrência de um não afeta a probabilidade do outro. Isso é expresso matematicamente como:
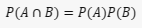
Se essa igualdade for verdadeira, então os eventos A e B são independentes. Caso contrário, eles não são independentes.
No entanto, na prática, muitas vezes não conhecemos as probabilidades exatas, então temos que estimá-las a partir dos dados. Se tivermos dados suficientes, podemos estimar as probabilidades e verificar se a igualdade acima é aproximadamente verdadeira.
Por exemplo, se estivermos jogando uma moeda (evento A) e um dado (evento B), e queremos verificar se os dois são independentes, poderíamos fazer o seguinte:
- Jogar a moeda e o dado várias vezes.
- Calcular a probabilidade estimada de cada evento e de ambos ocorrerem juntos.
- Verificar se P(A∩B)≈P(A)P(B).
Se a igualdade for aproximadamente verdadeira, então podemos concluir que os eventos são provavelmente independentes. Se não for, então eles provavelmente não são independentes.
Lembre-se de que essa é apenas uma estimativa. A única maneira de ter certeza absoluta da independência é conhecer todas as probabilidades exatas, o que raramente é possível na prática.
